I want to start by assuring you that this is no "fly by night" exploration. The following series is going to be challenging for us all. I’ve fled plenty of challenges in my life, but this is one that I’ve flocked to instead. The topic is geometry; the work is extensive, and this wisdom finds its way to feeling like a fresh start every time I sit down to share these ideas with a new audience.
I have removed as much complexity as intellectually possible in these early stages. My goal is not to overwhelm but to illuminate—to simplify where others may have complicated and to draw connections where others may have seen only disjointed ideas. I stand on the shoulders of many thinkers who have introduced similar concepts, but my aim is to highlight the synchronicity in their ideas and encourage you to dig deeper. We are on the cusp of what I believe is an alchemical renaissance in thought and application.
I’ve taken up the study of basic geometry in earnest, and I have a lifetime of discovery in front of me. What follows is a necessary re-evaluation of the very foundations of mathematical truth. It is also a call to rewire the way we think about them.
This method is grounded in unitary analysis and may very well change the way you conceptualize two-dimensional areas relative to unit side lengths. The import of these discoveries will take some time to assimilate, but for now, we start with a simplified view of coming attractions.
We are prone to accept the processes of investigation based on how we were originally taught. But what if there were a novel geometric approach that could transform our understanding of units and mathematics, one that defies the conventional methods ingrained in our minds? Imagine a method so revolutionary that it would necessitate the rewriting of every geometry textbook in circulation today. I realize I’m an early adopter of this approach, and for reasons I can’t always comprehend, I’m utterly captivated by triangles.
“Geometry is knowledge that appears to be produced by human beings, yet whose meaning is totally independent of them.”
And
"That one can work out forms which are seen purely inwardly, independently of the outer senses, gave me a feeling of deep contentment...To be able to grasp something purely spiritual brought me an inner joy. I know that through geometry I first experienced happiness."
Rudolf Steiner
Addressing Mathematical Fear
Before I continue, I want to address mathematical fear head-on because it’s crucial to create an environment where you, the reader, feel safe and supported as you explore these new theories without the burden of past learning experiences.
You know, that dreadful feeling that makes your stomach churn when you see a complicated equation or when someone even mentions the word 'algebra.’ If you've ever felt this way, you're not alone. Many of us were taught to memorize formulas and equations as if they were magic spells, and when those spells failed to work, we felt powerless, our confidence shattered. I’m here to tell you that it doesn’t have to be that way.
There’s a certain letting go that can assist you in absorbing new information. This approach is revolutionary in the sense that it can pave a new way to understand math—a way that could truly democratize the subject.
What's missing is the foundational grammar of math—the key that unlocks understanding and shatters fear. That key, my friends, is the equilateral triangle.
When I was in my high school geometry class, I observed how my classmates, who had struggled in other math courses, suddenly became active learners. They got it! The classroom was a buzz with excitement because, for the first time, many of these students had a geometric foundation that gave them the power to apply mathematical principles to visual problems. Once the students realized they had grammar—the basic building blocks—the entire course made sense to them. I had never before seen this level of engagement in any other math class. This geometry class left an indelible mark on me as I continued to pursue mathematical and scientific concepts.
Let me be clear: the hour is late. We can't afford to continue fearing a subject that has so much to offer. We're not just learning about shapes; we're setting the stage for an educational revolution—one where fear is replaced with curiosity and confusion with clarity.
Our journey through the world of equilateral triangles is not just for the mathematically inclined. It's for anyone who has ever looked at a problem and thought, 'There must be another way to understand this?” Well, there is! And it starts with a willingness to see the world differently—to see the world as it truly is. So let's roll up our sleeves, put our fears aside, and step into a new understanding of the universe.
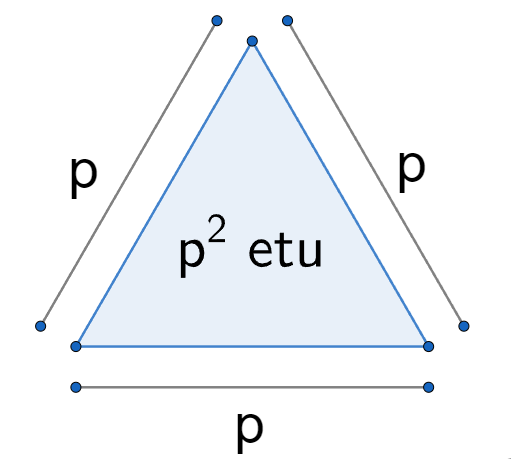
Introduction to the EquiTriangular Unit of Area (the etu) as Proposed by Wayne Roberts - Scale Structure Theory
Let an etu be a specific but relative unit of area:
Its absolute value may change, but it is defined to be always the area of an equilateral triangle of unitary side length.
The important point here is that units are related to other units, and, more particularly, that 'harmonics' exist as much in the field of mathematics and geometry as in music. Certain units 'mark out' resonances in the 'population of numbers and geometries.' The beautiful connections and resonances will become apparent as we enter through this gateway.”
Fig 1
Thus if the area of an equilateral triangle is defined to be 12etu, or more simply as 1 etu (i.e. 1 x 1, a unit of area), then its side-length is, by the same definition, 1 unit (i.e. one unit of length). The reverse is also true: If an equilateral triangle has sides of length 1 unit, its area is by definition, 1 etu.
Equilateral triangles can be dissected into p2 numbers-of-smaller-equilateral-triangular-units. And we can therefore express an equilateral triangle's area as being equal to p2 etu, in other words, that the number of etu's which fills its area without gaps is equal to p2, where p is the number of etu side-lengths which fit along a side of the equilateral triangle in question.
Fig 2
In equation form, The area of an equilateral triangle of side-length p (expressed in etu) =p2
Wayne Roberts - Scale Structure Theory
Traditional Method
Let's explore the differences between the conventional “square” approach and the method of calculating the area of equilateral triangles. Consider the area of an equilateral triangle with sides of unit length, expressed in square units. For most high school students, this might seem straightforward, but it's less intuitive compared to calculating the area using equitriangular units (etu), where the answer is simply p^2.
To illustrate the traditional method, we calculate the area of an equilateral triangle with a unitary side length, applying Pythagoras' Theorem. In square units, the area of any triangle is given by 1/2 bh where b is the base and h is the height from the apex to the base. By using Pythagoras' theorem, we find that h = √3/2. In decimal notion, √3/2 is equal to 0.433 . How rational is that?
The Traditional Solution is “Irrational”
Therefore, the area 1/2bh equals √3/4 square units. This result, an irrational number, demonstrates the mismatch that occurs when we use square units to measure a triangular space—much like trying to fit a square peg into a triangular hole. The calculation is cumbersome, complex, and ultimately less functional.
We’re not speaking to the absolute area (1/2 base times height); rather, we are working with relative self-similar shapes and the relative areas as they pertain to this same self-similar shape.
Who decided squares are actually “squares” anyway? It’s a convention. That all. Our Sapiedelic studies challenge convention. And we do like to place quotes around the word “square” not only for good measure but to highlight the flaw in the language. Regardless, we can work with it.
The implications of this new approach extend beyond mere calculation. They touch on how we visualize and interact with the world around us. Geometry, after all, is not just about numbers and shapes on a page; it’s about the very fabric of reality, the way we perceive space and structure in our daily lives.
Triangles are “SQUARES”
Fig 3
Area is now expressed in terms of ETU’s.
In Figure 1, we introduce the Equitriangular Unit (etu). In our Sapiedelic Studies, a Luminal Mind full of curiosity might ask the question, “What is a unit, and might we re-imagine a unit in terms of an equilateral triangle?” It should be understood that the triangle is the first 2-dimensional shape (created with straight lines) that encloses a volume and fills space without gaps. A triangle is the first form justifying the need to define an area. They have fractal-like properties, in that these self-similar forms can always be subdivided or multiplied to form smaller or larger triangle tessellation grids.
Most importantly, the idea that Triangles are “SQUARES” should turn your brain inside out. Most of us have always used actual squares (the one’s with 4-90° right angles) to represent squared numbered quantities, but what you see there in Figure 1 is just as valid and even more expressive. Now I’m getting ahead of myself again.
Fig 4
Notice that Fig 3 highlights a 3^2 field with 9 etu’s, Fig 4 highlights a 4^2 field that contains 16 etu’s, and Fig 5 below expands into a 5^2 field with 25 etu’s. Go ahead and check the number of triangles. Notice also the ODD number pattern that we have in all cases. In the example given in Fig 4, we add the first 4 ODD numbers to calculate 4x4.
1+3+5+7= 16
Fig 5
This pattern is a geometric expansion and continues on indefinitely. Five “Squared” is equal to 1+3+5+7+9 = 25 = 5^2, and there are other patterns to explain later on.
The reason why all this matters will become clear as our studies progress, but for now, it will suffice to say that “the successive summation of ODD numbers” always adds up to a squared number quantity. Again, we reiterate that Triangles are “Squares! “ We wish there was another word for “squares,” but that’s the language barrier rearing its ugly head again. We can’t use ‘triangular numbers’ because that term has already been used for another pattern. I speak to that here and echo many of the same themes discussed in this post below.
”Geometry is king, Math is okay, English sucks.” Kelvin Abraham - Tetryonics a.k.a. Tetryonic Theory
The Eutrigon
A eutrigon is a triangle with one angle equal to 60 degrees. Therefore, an equilateral triangle is a eutrigon. Let’s explore eutrigons of a different variety—triangles that are less regular.
Finding the Area of Any Eutrigon in Terms of ETU.
Let triangle ABC be any eutrigon. We define C to be the 60o angle, a and b to be the ‘legs’ or sides adjacent to C, and c the ‘hypotenuse’ or side opposite angle C.
Fig 6
The area of triangle ABC = Q
Mirror eutrigon ABC and orient the new eutrigon so that both copies share the same hypotenuse, c, with each other. This forms a parallelogram ADBC. By reasoning alone, these two eutrigons are congruent.
Fig 7
In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other. Roberts calls this a resonant scalar construction and likens this ‘move’ to completing an octave in music theory. We have parts, which form a symmetric whole, or’scale’ when they come together.
Thus, we know that the area of ADBC = 2Q
The Grandiosity of the Grander Odyssey
I’m going to let Wayne Roberts himself walk you through his grand finale.
“Now construct centrifugal (outward pointing) equilateral triangles on the legs of one of the component eutrigons.”
Fig 8
“It can be seen from an examination, that the construction has formed a large equilateral triangle DEF. Also we note that, in terms of areas,
ΔDEF = ΔACE + ΔBCF + 2Q
Applying our knowledge that the area of an equilateral triangle in etu is simply the side-length 'squared', or p2... we observe that…
ΔACE and ΔBCF are each equilateral triangles of side-lengths b and a respectively, and therefore their areas, expressed in terms of etu’s, are given by b2 and a2 respectively.
Thus, the equation above, expressed in etu, becomes:
Area of ΔDEF = a2 + b2 + 2Q
But
ΔDEF is equilateral and therefore its area in etu’s is its side-length 'squared'. Its side-length can be seen on inspection to be simply (a + b). Thus the area of
ΔDEF in etu is (a + b)2 . Substitution in the equation [immediately above] gives
(a + b)2 = a2 + b2 + 2Q
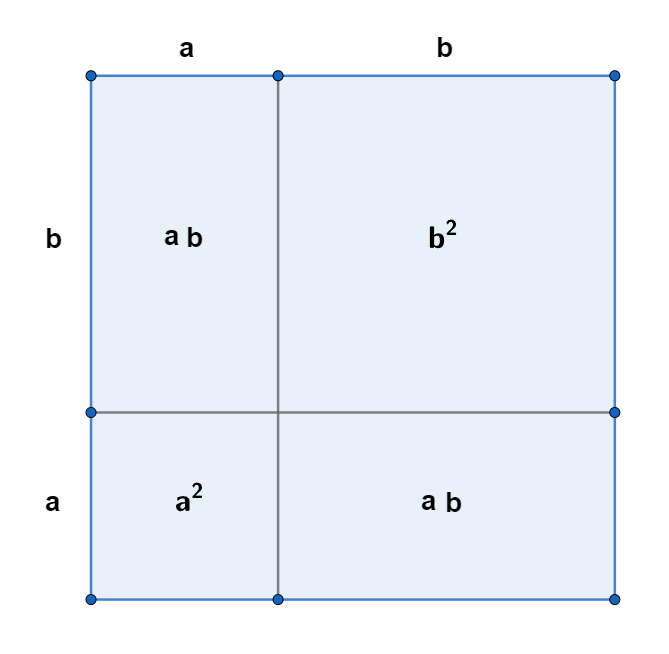
[Scale structure theory implies that there must be resonances or consonances between geometric scales and number scales (including the more generic numbers of algebra). Any student of algebra, learns very early on that the expansion of the expression (a + b)2 is equal to a2 + 2ab + b2. See Fig 9 for a scale-structural visual proof of this, but this time using the traditional square areas with which we are all so familiar]
Thus we accept that the term (a + b)2 is again equal to a2 + 2ab + b2, including triangular systems of analytic geometry. Thus, upon substitution of the expanded version of (a + b)2 in our equation above, we now have,
a2 + 2ab + b2 = a2 + b2 + 2Q
After cancelling corresponding terms on the left and right-hand sides of the above equation, we have simply:
2ab = 2Q
dividing both sides by 2, this equation reduces to the elegant identity [expressed in terms of relative units, in this case, etu],
area Q = ab
Thus, the area of any eutrigonexpressed in etu is ab, where a and b are the lengths of its legs (namely those sides adjacent to the 60-degree angle,
Areaeutrigon = ab
Fig 9
(a + b)^2 = (a + b)(a + b) = a^2 + ab + ab + b^2 = a^2 + 2ab + b^2
Traditional view of the geometric solution to ( a + b ) ^ 2
Simultaneously Checking our Work Geometrically and Mathematically
ΔDEF = ΔACE + ΔBCF + 2Q
The area of ΔDEF = a^2 + b^2 + 2Q
Let a = 2 and b = 5. We’ve added an isometric grid underneath the form so we can easily count unit triangles.
a^2 = 2^2 = 4 b^2 = 5^2 = 25
We know that the side lengths of the large triangle is a + b = 2 + 5 = 7 Therefore, we have a 7^2 tessellation, which = 49
The legs of eutrigon ABD are 2 and 5, just as the legs of eutrigon ABC are also 2 and 5.
Our work above states that the Areaeutrigon Q= ab = 2 x 5 = 10
a^2 = 4 b^2 = 25 2Q = 20
a^2 + b^2 + 2Q = 4 + 25 + 20 = 49 = 7^2
Checks out to me!
Fig 10
A Glimpse into the Future of Geometry
As we move forward, I will guide you through a series of explorations that challenge conventional thinking and open up new possibilities. We’ll begin with the basics, ensuring that everyone can follow along, but we’ll quickly move into deeper waters.
The concepts we’ll discuss may take time to fully understand, but I believe they have the power to revolutionize the way we think about math and its role in our lives.
This journey is not just for mathematicians or scholars; it’s for anyone with a curious mind and a willingness to explore. Whether you’re a seasoned mathematician or someone who has always struggled with the subject, I believe you’ll find something of value here.
Let’s rewrite the way we think about geometry and, in doing so, open the door to new regions of understanding and possibility.
Δ Δ Δ Namaste, No mistake, In the lucidic wake, We stand in awe. Δ Δ Δ
If your brain hasn’t melted by now, we’ll get you on the next one!
brilliant introduction to the integrity of spherical thinking as it relates to the areal accounting by triangling. i am looking forward to what may follow.
may i ask: why wouldn't one just replace the "square" in a "squared area" with the triangle, too? so two to the second power, two triangled, is four.
brilliant introduction to the integrity of spherical thinking as it relates to the areal accounting by triangling. i am looking forward to what may follow.
may i ask: why wouldn't one just replace the "square" in a "squared area" with the triangle, too? so two to the second power, two triangled, is four.
and on a related note, sphere are a few more reasons why a triangular paradigmshift may be very reasonable: https://youtu.be/AZF8zg9xTtA?si=H1xSawwAcXj9Ik2z
peace
struppi